C# Binary Search Tree Implementation
This example shows how to implement a Binary Search Tree using C#. A tree whose nodes have at most 2 child nodes is called a binary tree. we name them the left and right child because each node in a binary tree can have only 2 children.
A sample binary tree:
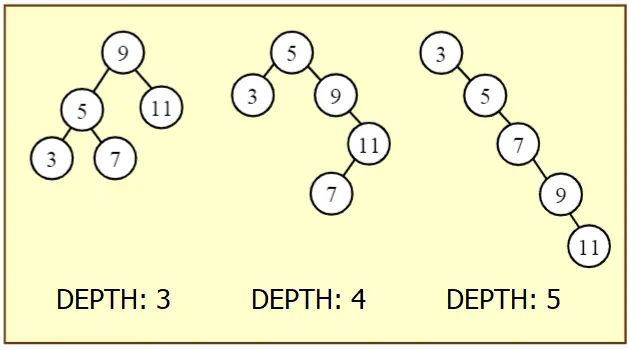
Tree Traversals (PreOrder, InOrder, PostOrder)
Traversal is a process to visit all the nodes of a tree. In this example, I implemented three method which we use to traverse a tree.
- PreOrder Traversal
- InOrder Traversal
- PostOrder Traversal
PreOrder Traversal:
- Visit the root
- Traverse the left subtree
- Traverse the right subtree
InOrder Traversal:
- Traverse the left subtree
- Visit the root
- Traverse the right subtree
PostOrder Traversal:
- Traverse the left subtree
- Traverse the right subtree
- Visit the root
All source code is below.
Node Class:
class Node
{
public Node LeftNode { get; set; }
public Node RightNode { get; set; }
public int Data { get; set; }
}
BinaryTree Class:
class BinaryTree
{
public Node Root { get; set; }
public bool Add(int value)
{
Node before = null, after = this.Root;
while (after != null)
{
before = after;
if (value < after.Data) //Is new node in left tree?
after = after.LeftNode;
else if (value > after.Data) //Is new node in right tree?
after = after.RightNode;
else
{
//Exist same value
return false;
}
}
Node newNode = new Node();
newNode.Data = value;
if (this.Root == null)//Tree ise empty
this.Root = newNode;
else
{
if (value < before.Data)
before.LeftNode = newNode;
else
before.RightNode = newNode;
}
return true;
}
public Node Find(int value)
{
return this.Find(value, this.Root);
}
public void Remove(int value)
{
this.Root = Remove(this.Root, value);
}
private Node Remove(Node parent, int key)
{
if (parent == null) return parent;
if (key < parent.Data) parent.LeftNode = Remove(parent.LeftNode, key); else if (key > parent.Data)
parent.RightNode = Remove(parent.RightNode, key);
// if value is same as parent's value, then this is the node to be deleted
else
{
// node with only one child or no child
if (parent.LeftNode == null)
return parent.RightNode;
else if (parent.RightNode == null)
return parent.LeftNode;
// node with two children: Get the inorder successor (smallest in the right subtree)
parent.Data = MinValue(parent.RightNode);
// Delete the inorder successor
parent.RightNode = Remove(parent.RightNode, parent.Data);
}
return parent;
}
private int MinValue(Node node)
{
int minv = node.Data;
while (node.LeftNode != null)
{
minv = node.LeftNode.Data;
node = node.LeftNode;
}
return minv;
}
private Node Find(int value, Node parent)
{
if (parent != null)
{
if (value == parent.Data) return parent;
if (value < parent.Data)
return Find(value, parent.LeftNode);
else
return Find(value, parent.RightNode);
}
return null;
}
public int GetTreeDepth()
{
return this.GetTreeDepth(this.Root);
}
private int GetTreeDepth(Node parent)
{
return parent == null ? 0 : Math.Max(GetTreeDepth(parent.LeftNode), GetTreeDepth(parent.RightNode)) + 1;
}
public void TraversePreOrder(Node parent)
{
if (parent != null)
{
Console.Write(parent.Data + " ");
TraversePreOrder(parent.LeftNode);
TraversePreOrder(parent.RightNode);
}
}
public void TraverseInOrder(Node parent)
{
if (parent != null)
{
TraverseInOrder(parent.LeftNode);
Console.Write(parent.Data + " ");
TraverseInOrder(parent.RightNode);
}
}
public void TraversePostOrder(Node parent)
{
if (parent != null)
{
TraversePostOrder(parent.LeftNode);
TraversePostOrder(parent.RightNode);
Console.Write(parent.Data + " ");
}
}
}
Sample Application:
BinaryTree binaryTree = new BinaryTree();
binaryTree.Add(1);
binaryTree.Add(2);
binaryTree.Add(7);
binaryTree.Add(3);
binaryTree.Add(10);
binaryTree.Add(5);
binaryTree.Add(8);
Node node = binaryTree.Find(5);
int depth = binaryTree.GetTreeDepth();
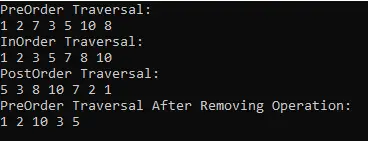
Console.WriteLine("PreOrder Traversal:");
binaryTree.TraversePreOrder(binaryTree.Root);
Console.WriteLine();
Console.WriteLine("InOrder Traversal:");
binaryTree.TraverseInOrder(binaryTree.Root);
Console.WriteLine();
Console.WriteLine("PostOrder Traversal:");
binaryTree.TraversePostOrder(binaryTree.Root);
Console.WriteLine();
binaryTree.Remove(7);
binaryTree.Remove(8);
Console.WriteLine("PreOrder Traversal After Removing Operation:");
binaryTree.TraversePreOrder(binaryTree.Root);
Console.WriteLine();
Console.ReadLine();
See Also:
C# Binary Search Example

thanks for this articles
Your implementation doesn’t work because you commented out some of the code on line 12.
It should be:
12:
if (value after.Data) //Is new node in right tree?
after = after.RightNode;
Here is a modified version with the fix, and some additional code for testing:
/**
* Original Author Turgay, http://csharpexamples.com/c-binary-search-tree-implementation/
* Modified by Paul Mehta 2019/11/05
**/
using System;
using System.Collections.Generic;
namespace InterviewPrep
{
public class BinaryTreeTest
{
static void TestBinaryTree(int[] values)
{
BinaryTree bt = new BinaryTree(values);
Console.WriteLine(” Depth: ” + bt.GetTreeDepth());
bt.TraverseInOrder();
bt.TraversePreOrder();
bt.TraversePostOrder();
if (values.Length >= 2)
{
Console.WriteLine(” Removing value { ” + values[1] + ” }”);
bt.Remove(values[1]);
bt.TraverseInOrder();
bt.TraversePreOrder();
bt.TraversePostOrder();
}
Console.WriteLine(“\n”);
}
public static void Main(string[] args)
{
int[] arr1 = { 1, 2, 7, 3, 10, 5, 8, 8, 9 };
int[] arr2 = { 1, 3, 6, 2, 7, 5, 4, 8, 9 };
int[] arr3 = { -10, 10, -20, 0, 17, 19, 4, 8, 9, -30, -5 };
TestBinaryTree(arr1);
TestBinaryTree(arr2);
TestBinaryTree(arr3);
Console.ReadLine();
}
}
class Node
{
public Node LeftNode { get; set; }
public Node RightNode { get; set; }
public int Data { get; set; }
}
class BinaryTree
{
public BinaryTree()
{
}
public BinaryTree(int[] values)
{
Console.WriteLine(“BinaryTree { ” + string.Join(“,”, values) + ” }”);
foreach (int i in values)
{
Add(i);
}
}
public Node Root { get; set; }
public bool Add(int value)
{
Node before = null, after = this.Root;
while (after != null)
{
before = after;
if (value after.Data) //Is new node in right tree?
after = after.RightNode;
else
{
//Exist same value
return false;
}
}
Node newNode = new Node();
newNode.Data = value;
if (this.Root == null)//Tree ise empty
this.Root = newNode;
else
{
if (value < before.Data)
before.LeftNode = newNode;
else
before.RightNode = newNode;
}
return true;
}
public Node Find(int value)
{
return this.Find(value, this.Root);
}
public void Remove(int value)
{
Remove(this.Root, value);
}
private Node Remove(Node parent, int key)
{
if (parent == null) return parent;
if (key parent.Data)
parent.RightNode = Remove(parent.RightNode, key);
// if value is same as parent’s value, then this is the node to be deleted
else
{
// node with only one child or no child
if (parent.LeftNode == null)
return parent.RightNode;
else if (parent.RightNode == null)
return parent.LeftNode;
// node with two children: Get the inorder successor (smallest in the right subtree)
parent.Data = MinValue(parent.RightNode);
// Delete the inorder successor
parent.RightNode = Remove(parent.RightNode, parent.Data);
}
return parent;
}
private int MinValue(Node node)
{
int minv = node.Data;
while (node.LeftNode != null)
{
minv = node.LeftNode.Data;
node = node.LeftNode;
}
return minv;
}
private Node Find(int value, Node parent)
{
if (parent != null)
{
if (value == parent.Data) return parent;
if (value < parent.Data)
return Find(value, parent.LeftNode);
else
return Find(value, parent.RightNode);
}
return null;
}
public int GetTreeDepth()
{
return this.GetTreeDepth(this.Root);
}
private int GetTreeDepth(Node parent)
{
return parent == null ? 0 : Math.Max(GetTreeDepth(parent.LeftNode), GetTreeDepth(parent.RightNode)) + 1;
}
public void TraversePreOrder()
{
Console.Write(" Traverse Pre Order: \t");
TraversePreOrder(this.Root);
Console.WriteLine();
}
public void TraversePreOrder(Node parent)
{
if (parent != null)
{
Console.Write(parent.Data + " ");
TraversePreOrder(parent.LeftNode);
TraversePreOrder(parent.RightNode);
}
}
public void TraverseInOrder()
{
Console.Write(" Traverse In Order: \t");
TraverseInOrder(this.Root);
Console.WriteLine();
}
public void TraverseInOrder(Node parent)
{
if (parent != null)
{
TraverseInOrder(parent.LeftNode);
Console.Write(parent.Data + " ");
TraverseInOrder(parent.RightNode);
}
}
public void TraversePostOrder()
{
Console.Write(" Traverse Post Order: \t");
TraversePostOrder(this.Root);
Console.WriteLine();
}
public void TraversePostOrder(Node parent)
{
if (parent != null)
{
TraversePostOrder(parent.LeftNode);
TraversePostOrder(parent.RightNode);
Console.Write(parent.Data + " ");
}
}
}
}
Thanks for reply. I accidentally commented out some of the code. Bug fixed.
very clear code! thank you
I have small doubt about the code,
when you assign condition, for Root node. on line 26
if (this.Root == null)//Tree is empty
this.Root = newNode;
this does not have properties of RightNode or LeftNode Object which is null.
So the program will crash on second iteration, because when you check on line 12 the object of afterLeftNode is NULL
if (value after.Data) //Is new node in right tree?
after = after.RightNode;
another question should ask also, is it the root is purposely not define
the LeftNode or RightNode
?
– Please test the code. It runs.
– Root node is initial/root node(It is not a left or right node of an another node).
Thank you so much for your code. It is really helpful.
But there is one major problem.
The value at the root will never be deleted.
In your sample, 1 cannot be deleted. Could you fix it please
At line 46, should be
Root = Remove(this.Root, value);
Thanks for your support. I fixed it.
Hi, Thank for ur code.
But I don’t remove first node input.
Ex: binaryTree.Remove(1);
Hi, thanks so much for the code. Could I ask, how do you print out the depth and whether or not an element is in the tree? (sorry if this seems really basic haha)
This is how I implemented the adding logic(with a little recursion it’s more friendly 🙂 )
public bool Add(int value)
{
var newNode = new Node {Data = value};
if (Root == null)
{
Root = newNode;
return true;
}
return AddChildNode(newNode, Root);
}
private bool AddChildNode(Node newNode, Node parent)
{
if (newNode.Data > parent.Data)
{
if (parent.RightNode == null)
parent.RightNode = newNode;
else
AddChildNode(newNode, parent.RightNode);
}
else
{
if (parent.LeftNode == null)
parent.LeftNode = newNode;
else
AddChildNode(newNode, parent.LeftNode);
}
return true;
}
Hi turgay, thank you very much for your efforts and the code! I was looking for a binary search tree library but couldn’t find a package for my needs. Finally, I have implemented one from scratch: https://github.com/m31coding/M31.BinarySearchTrees
I hope it is okay if I just leave the link here, it might be useful for others.
Best regards,
Kevin