This example shows how to implement a Binary Search Tree using  C#. A tree whose nodes have at most 2 child nodes is called a binary tree. we name them the left and right child because each node in a binary tree can have only 2 children.
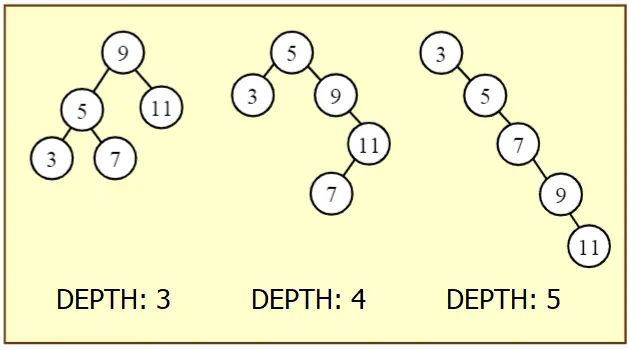
A sample binary tree:

Tree Traversals (PreOrder, InOrder, PostOrder)

Traversal is a process to visit all the nodes of a tree. In this example, I implemented three method which we use to traverse a tree.

• PreOrder Traversal
• InOrder Traversal
• PostOrder Traversal

PreOrder Traversal:

• Visit the root
• Traverse the left subtree
• Traverse the right subtree

InOrder Traversal:

• Traverse the left subtree
• Visit the root
• Traverse the right subtree

PostOrder Traversal:

• Traverse the left subtree
• Traverse the right subtree
• Visit the root

All source code is below.
Node Class:

        
    class Node
    {
        public Node LeftNode { get; set; }
        public Node RightNode { get; set; }
        public int Data { get; set; }
    }

BinaryTree Class:

        
    class BinaryTree
    {
        public Node Root { get; set; }

        public bool Add(int value)
        {
            Node before = null, after = this.Root;

            while (after != null)
            {
                before = after;
                if (value < after.Data) //Is new node in left tree? 
                      after = after.LeftNode; 
                else if (value > after.Data) //Is new node in right tree?
                    after = after.RightNode;
                else
                {
                    //Exist same value
                    return false;
                }
            }

            Node newNode = new Node();
            newNode.Data = value;

            if (this.Root == null)//Tree ise empty
                this.Root = newNode;
            else
            {
                if (value < before.Data)
                    before.LeftNode = newNode;
                else
                    before.RightNode = newNode;
            }

            return true;
        }

        public Node Find(int value)
        {
            return this.Find(value, this.Root);            
        }

        public void Remove(int value)
        {
            this.Root = Remove(this.Root, value);
        }

        private Node Remove(Node parent, int key)
        {
            if (parent == null) return parent;

            if (key < parent.Data) parent.LeftNode = Remove(parent.LeftNode, key); else if (key > parent.Data)
                parent.RightNode = Remove(parent.RightNode, key);

            // if value is same as parent's value, then this is the node to be deleted  
            else
            {
                // node with only one child or no child  
                if (parent.LeftNode == null)
                    return parent.RightNode;
                else if (parent.RightNode == null)
                    return parent.LeftNode;

                // node with two children: Get the inorder successor (smallest in the right subtree)  
                parent.Data = MinValue(parent.RightNode);

                // Delete the inorder successor  
                parent.RightNode = Remove(parent.RightNode, parent.Data);
            }

            return parent;
        }

        private int MinValue(Node node)
        {
            int minv = node.Data;

            while (node.LeftNode != null)
            {
                minv = node.LeftNode.Data;
                node = node.LeftNode;
            }

            return minv;
        }

        private Node Find(int value, Node parent)
        {
            if (parent != null)
            {
                if (value == parent.Data) return parent;
                if (value < parent.Data)
                    return Find(value, parent.LeftNode);
                else
                    return Find(value, parent.RightNode);
            }

            return null;
        }

        public int GetTreeDepth()
        {
            return this.GetTreeDepth(this.Root);
        }

        private int GetTreeDepth(Node parent)
        {
            return parent == null ? 0 : Math.Max(GetTreeDepth(parent.LeftNode), GetTreeDepth(parent.RightNode)) + 1;
        }

        public void TraversePreOrder(Node parent)
        {
            if (parent != null)
            {
                Console.Write(parent.Data + " ");
                TraversePreOrder(parent.LeftNode);
                TraversePreOrder(parent.RightNode);
            }
        }

        public void TraverseInOrder(Node parent)
        {
            if (parent != null)
            {
                TraverseInOrder(parent.LeftNode);
                Console.Write(parent.Data + " ");
                TraverseInOrder(parent.RightNode);
            }
        }

        public void TraversePostOrder(Node parent)
        {
            if (parent != null)
            {
                TraversePostOrder(parent.LeftNode);
                TraversePostOrder(parent.RightNode);
                Console.Write(parent.Data + " ");
            }
        }
    }

Sample Application:

        
            BinaryTree binaryTree = new BinaryTree();

            binaryTree.Add(1);
            binaryTree.Add(2);
            binaryTree.Add(7);
            binaryTree.Add(3);
            binaryTree.Add(10);
            binaryTree.Add(5);
            binaryTree.Add(8);

            Node node = binaryTree.Find(5);
            int depth = binaryTree.GetTreeDepth();

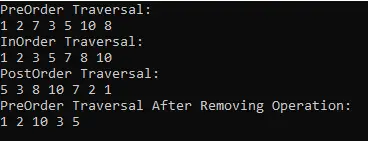
            Console.WriteLine("PreOrder Traversal:");
            binaryTree.TraversePreOrder(binaryTree.Root);
            Console.WriteLine();

            Console.WriteLine("InOrder Traversal:");
            binaryTree.TraverseInOrder(binaryTree.Root);
            Console.WriteLine();

            Console.WriteLine("PostOrder Traversal:");
            binaryTree.TraversePostOrder(binaryTree.Root);
            Console.WriteLine();

            binaryTree.Remove(7);
            binaryTree.Remove(8);

            Console.WriteLine("PreOrder Traversal After Removing Operation:");
            binaryTree.TraversePreOrder(binaryTree.Root);
            Console.WriteLine();

            Console.ReadLine();

Program output:

See Also:
C# Binary Search Example