08 Haz

Select XML Nodes by Name or Attribute Value in C#

To locate specific elements within an XML document, XPath expressions are commonly used. The SelectNodes method of the XmlNode class retrieves a collection of nodes that match a given XPath query. On the other hand, the SelectSingleNode method returns only the first node that satisfies the specified XPath condition.

Let’s assume we have the following XML structure as an example.

<Names>
    <Name type="M">
        <FirstName>Lionel</FirstName>
        <LastName>Messi</LastName>
    </Name>
    <Name type="M">
        <FirstName>Cristiano</FirstName>
        <LastName>Ronaldo</LastName>
    </Name>
    <Name type="F">
        <FirstName>Maria</FirstName>
        <LastName>Sharapova</LastName>
    </Name>
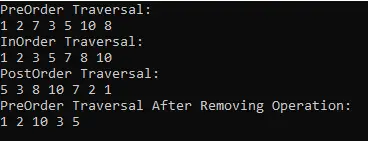
</Names>

To retrieve all <Name> elements from an XML document, you can use the XPath query /Names/Name. The leading slash / indicates that the <Names> element must be the root of the XML structure. By calling the SelectNodes method, you’ll receive an XmlNodeList containing all matching <Name> nodes. If you need to access the value of a child element like <FirstName>, you can do so by indexing the parent XmlNode with the tag name—for example: xmlNode[“FirstName”].InnerText. Here’s a sample code snippet to illustrate this approach.

// Create an XmlDocument object and load the XML data
XmlDocument xmlDoc = new XmlDocument();
xmlDoc.LoadXml(xmlData);

// Use XPath to select all <Name> nodes under the root <Names> element
XmlNodeList nameNodes = xmlDoc.SelectNodes("/Names/Name");

// Loop through each <Name> node in the list
foreach (XmlNode nameNode in nameNodes)
{
     // Access the <FirstName> and <LastName> child nodes and get their values
     string firstName = nameNode["FirstName"]?.InnerText;
     string lastName = nameNode["LastName"]?.InnerText;
     Console.WriteLine($"First Name: {firstName}, Last Name: {lastName}");
}

To get all name nodes use XPath expression /Names/Name. To get only male names (to select all nodes with specific XML attribute) use XPath expression /Names/Name[@type='M'].

XmlDocument xml = new XmlDocument();
xml.LoadXml(str);  // suppose that str string contains "<Names>...</Names>"

XmlNodeList xnList = xml.SelectNodes("/Names/Name[@type='M']");
foreach (XmlNode xn in xnList)
{
  Console.WriteLine(xn.InnerText);
}

02 May

C# Binary Search Tree Implementation

This example shows how to implement a Binary Search Tree using  C#. A tree whose nodes have at most 2 child nodes is called a binary tree. we name them the left and right child because each node in a binary tree can have only 2 children.
A sample binary tree:
binary tree 2

Tree Traversals (PreOrder, InOrder, PostOrder)

Traversal is a process to visit all the nodes of a tree. In this example, I implemented three method which we use to traverse a tree.

  • PreOrder Traversal
  • InOrder Traversal
  • PostOrder Traversal

PreOrder Traversal:

  • Visit the root
  • Traverse the left subtree
  • Traverse the right subtree

InOrder Traversal:

  • Traverse the left subtree
  • Visit the root
  • Traverse the right subtree

PostOrder Traversal:

  • Traverse the left subtree
  • Traverse the right subtree
  • Visit the root

All source code is below.
Node Class:

        
    class Node
    {
        public Node LeftNode { get; set; }
        public Node RightNode { get; set; }
        public int Data { get; set; }
    }

BinaryTree Class:

        
    class BinaryTree
    {
        public Node Root { get; set; }

        public bool Add(int value)
        {
            Node before = null, after = this.Root;

            while (after != null)
            {
                before = after;
                if (value < after.Data) //Is new node in left tree? 
                      after = after.LeftNode; 
                else if (value > after.Data) //Is new node in right tree?
                    after = after.RightNode;
                else
                {
                    //Exist same value
                    return false;
                }
            }

            Node newNode = new Node();
            newNode.Data = value;

            if (this.Root == null)//Tree ise empty
                this.Root = newNode;
            else
            {
                if (value < before.Data)
                    before.LeftNode = newNode;
                else
                    before.RightNode = newNode;
            }

            return true;
        }

        public Node Find(int value)
        {
            return this.Find(value, this.Root);            
        }

        public void Remove(int value)
        {
            this.Root = Remove(this.Root, value);
        }

        private Node Remove(Node parent, int key)
        {
            if (parent == null) return parent;

            if (key < parent.Data) parent.LeftNode = Remove(parent.LeftNode, key); else if (key > parent.Data)
                parent.RightNode = Remove(parent.RightNode, key);

            // if value is same as parent's value, then this is the node to be deleted  
            else
            {
                // node with only one child or no child  
                if (parent.LeftNode == null)
                    return parent.RightNode;
                else if (parent.RightNode == null)
                    return parent.LeftNode;

                // node with two children: Get the inorder successor (smallest in the right subtree)  
                parent.Data = MinValue(parent.RightNode);

                // Delete the inorder successor  
                parent.RightNode = Remove(parent.RightNode, parent.Data);
            }

            return parent;
        }

        private int MinValue(Node node)
        {
            int minv = node.Data;

            while (node.LeftNode != null)
            {
                minv = node.LeftNode.Data;
                node = node.LeftNode;
            }

            return minv;
        }

        private Node Find(int value, Node parent)
        {
            if (parent != null)
            {
                if (value == parent.Data) return parent;
                if (value < parent.Data)
                    return Find(value, parent.LeftNode);
                else
                    return Find(value, parent.RightNode);
            }

            return null;
        }

        public int GetTreeDepth()
        {
            return this.GetTreeDepth(this.Root);
        }

        private int GetTreeDepth(Node parent)
        {
            return parent == null ? 0 : Math.Max(GetTreeDepth(parent.LeftNode), GetTreeDepth(parent.RightNode)) + 1;
        }

        public void TraversePreOrder(Node parent)
        {
            if (parent != null)
            {
                Console.Write(parent.Data + " ");
                TraversePreOrder(parent.LeftNode);
                TraversePreOrder(parent.RightNode);
            }
        }

        public void TraverseInOrder(Node parent)
        {
            if (parent != null)
            {
                TraverseInOrder(parent.LeftNode);
                Console.Write(parent.Data + " ");
                TraverseInOrder(parent.RightNode);
            }
        }

        public void TraversePostOrder(Node parent)
        {
            if (parent != null)
            {
                TraversePostOrder(parent.LeftNode);
                TraversePostOrder(parent.RightNode);
                Console.Write(parent.Data + " ");
            }
        }
    }

Sample Application:

        
            BinaryTree binaryTree = new BinaryTree();

            binaryTree.Add(1);
            binaryTree.Add(2);
            binaryTree.Add(7);
            binaryTree.Add(3);
            binaryTree.Add(10);
            binaryTree.Add(5);
            binaryTree.Add(8);

            Node node = binaryTree.Find(5);
            int depth = binaryTree.GetTreeDepth();

            Console.WriteLine("PreOrder Traversal:");
            binaryTree.TraversePreOrder(binaryTree.Root);
            Console.WriteLine();

            Console.WriteLine("InOrder Traversal:");
            binaryTree.TraverseInOrder(binaryTree.Root);
            Console.WriteLine();

            Console.WriteLine("PostOrder Traversal:");
            binaryTree.TraversePostOrder(binaryTree.Root);
            Console.WriteLine();

            binaryTree.Remove(7);
            binaryTree.Remove(8);

            Console.WriteLine("PreOrder Traversal After Removing Operation:");
            binaryTree.TraversePreOrder(binaryTree.Root);
            Console.WriteLine();

            Console.ReadLine();

Program output:
binary tree output

See Also:
C# Binary Search Example

29 Mar

Select,Insert,Update,Delete Data in Access File using C#

This example shows how to insert ,update, delete and select data in Access File(CRUD Operations).

TABLE1:

ID NAME SURNAME
1 Jack Sparrow

Select Command Example:

            
            string mdfFile = @"csharpexamples.mdb";

            using (OleDbConnection connection = new OleDbConnection(string.Format("Provider=Microsoft.Jet.OLEDB.4.0;Data Source={0}", mdfFile)))
            {
                using (OleDbCommand selectCommand = new OleDbCommand("SELECT TOP 10 * FROM TABLE1", connection))
                {
                    connection.Open();

                    DataTable table = new DataTable();
                    OleDbDataAdapter adapter = new OleDbDataAdapter();
                    adapter.SelectCommand = selectCommand;
                    adapter.Fill(table);

                    foreach (DataRow row in table.Rows)
                    {
                        object nameValue = row["NAME"];
                        object surnameValue = row["SURNAME"];
                    }
                }
            }

Insert Command Example:

            
            string mdfFile = @"csharpexamples.mdb";

            using (OleDbConnection connection = new OleDbConnection(string.Format("Provider=Microsoft.Jet.OLEDB.4.0;Data Source={0}", mdfFile)))
            {
                using (OleDbCommand insertCommand = new OleDbCommand("INSERT INTO TABLE1 ([NAME],[SURNAME]) VALUES (?,?)", connection))
                {
                    connection.Open();

                    insertCommand.Parameters.AddWithValue("@NAME", "Brad");
                    insertCommand.Parameters.AddWithValue("@SURNAME", "Pitt");

                    insertCommand.ExecuteNonQuery();
                }
            }

Update Command Example:

      
            string mdfFile = @"csharpexamples.mdb";

            using (OleDbConnection connection = new OleDbConnection(string.Format("Provider=Microsoft.Jet.OLEDB.4.0;Data Source={0}", mdfFile)))
            {
                using (OleDbCommand updateCommand = new OleDbCommand("UPDATE TABLE1 SET [NAME] = ?, [SURNAME] = ? WHERE [ID] = ?", connection))
                {
                    connection.Open();

                    updateCommand.Parameters.AddWithValue("@NAME", "Brad2");
                    updateCommand.Parameters.AddWithValue("@SURNAME", "Pitt2");
                    updateCommand.Parameters.AddWithValue("@ID", 2);

                    updateCommand.ExecuteNonQuery();
                }
            }

Delete Command Example:

            
            string mdfFile = @"csharpexamples.mdb";

            using (OleDbConnection connection = new OleDbConnection(string.Format("Provider=Microsoft.Jet.OLEDB.4.0;Data Source={0}", mdfFile)))
            {
                using (OleDbCommand deleteCommand = new OleDbCommand("DELETE FROM TABLE1 WHERE [ID] = ?", connection))
                {
                    connection.Open();

                    deleteCommand.Parameters.AddWithValue("@ID", 2);

                    deleteCommand.ExecuteNonQuery();
                }
            }

See Also: Select,Insert,Update,Delete Data in MySQL using C#

27 Mar

C# Collections Tutorial

This tutorial contains the information about C# Collection types.

  • Collections are similar to Arrays, providing a more flexible way to work with an object group.
  • You would have noticed in arrays that you must define in advance the number of elements in an array. When the array was declared, this had to be done. But you don’t need to define the size of the collection in advance in a collection. Elements can be added or even removed from the collection at any time.
Collection Description
ArrayList The ArrayList is similar to the C# array data type. The greatest difference is the dynamic nature of the collection of array list.
Stack The stack represents a simple last-in-first-out (LIFO) non-generic collection of objects.
Queue The Queue is a special collection which represents first-in, first-out concept of objects.
Hashtable A hash table is a collection that is used to store key-value pairs.
27 Mar

C# ArrayList Example

The ArrayList is similar to the C# array data type. The greatest difference is the dynamic nature of the collection of array list.

  • The add method is used to add an element to the ArrayList.

ArrayList Example:

ArrayList arrayList = new ArrayList();
arrayList.Add("Element 1");
arrayList.Add("Element 2");
arrayList.Add("Element 3");

Console.WriteLine("ArrayList Count: " + arrayList.Count);
Console.WriteLine("Contains Element2: " + arrayList.Contains("Element 2"));
arrayList.Remove("Element 2");
Console.WriteLine("ArrayList Count: " + arrayList.Count);

Program Output:
array list output